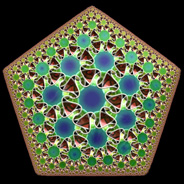
Hyperbolic geometry can be very beautiful. Hyperbolic tilings are not technically fractals, but they appear as fractals when you look at them (because they must be projected into Euclidean space).
(12,4) Poincaré Ball - POV-Ray 3.6.1, 5/27/11

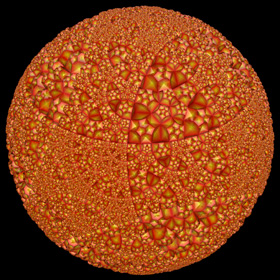 The Poincaré ball is the 3D analogy of the Poincaré disk. It is a projection of uniformly tiled hyperbolic polyhedrons from hyperbolic space into Euclidean space. This projection can be generated by recursively applying spherical inversions to the faces of a sphairahedron (a polyhedron with spherical faces). This is a (12,4) Poincaré ball, meaning that is was generated from a hyperbolic dodecahedron having 12 faces with 4 dodecahedrons meeting at each edge. You can purchase this as a poster here.
The Poincaré ball is the 3D analogy of the Poincaré disk. It is a projection of uniformly tiled hyperbolic polyhedrons from hyperbolic space into Euclidean space. This projection can be generated by recursively applying spherical inversions to the faces of a sphairahedron (a polyhedron with spherical faces). This is a (12,4) Poincaré ball, meaning that is was generated from a hyperbolic dodecahedron having 12 faces with 4 dodecahedrons meeting at each edge. You can purchase this as a poster here. |
 Here is the Poincaré ball viewed from the inside.
Here is the Poincaré ball viewed from the inside.Links article on 3D hyperbolic tilings - by Vladimir Bulatov Hyperbolic Tesselations in 3D - by Jos Leys Curved Spaces 3 - program for tiling spherical and hyperbolic 3D space, by Jeff Weeks Hyperbolic Space Tiled by Dodecahedra - by Charlie Gunn Convex Uniform Honeycombs in Hyperbolic Space - Wikipedia article Icosahedral Honeycomb, Order-5 Cubic Honeycomb - by Claudio Rocchini |
(7,3) Poincaré Hyperbolic Tiling - AutoLisp, POV-Ray 3.6.1, 4/28/11
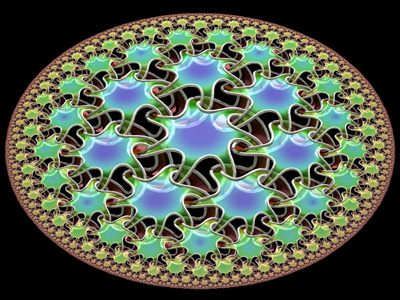
 These are (7,3) Poincaré hyperbolic tilings, meaning that each tile is a 7-sided polygon, and 3 polygons meet at each vertex. In real life (that is to say, in Euclidean space), it would be impossible to cover a plane with 7-sided polygons, but in hyperbolic space this is possible. These tilings were generated using a series of reflections called anti-homographies. I learned about homographies while participating at the Experimental Geometry Lab at the University of Maryland. Here is some Mathematica code:
These are (7,3) Poincaré hyperbolic tilings, meaning that each tile is a 7-sided polygon, and 3 polygons meet at each vertex. In real life (that is to say, in Euclidean space), it would be impossible to cover a plane with 7-sided polygons, but in hyperbolic space this is possible. These tilings were generated using a series of reflections called anti-homographies. I learned about homographies while participating at the Experimental Geometry Lab at the University of Maryland. Here is some Mathematica code:(* runtime: 2 seconds *) n = 7; m = 3; dt = 2Pi/n; dtm = 2Pi/m;r = 1.0/(1 - Sin[dt/2]/Cos[dtm/2]); R = r Cos[(dt + dtm)/2]/Cos[dtm/2]; ToMatrix[z_, r_] := (I/r) {{z, r^2 - z Conjugate[z]}, {1, -Conjugate[z]}}; alist = Table[ToMatrix[r Exp[I t],r - 1], {t, dt/2, 2 Pi, dt}]; Tlist = Join[{IdentityMatrix[2]}, alist]; homography[{{a_, b_}, {c_, d_}}, z_] := (a z + b)/(c z + d); FindT[T0_, Tlist_] := MemberQ[Tlist, T_ /; Abs[homography[T, 0] - homography[T0, 0]] < 1.0*^-3]; i2 = 1; Do[i1 = i2 + 1; i2 = Length[Tlist]; Do[Scan[(T = Tlist[[i]].#; If[! FindT[T, Tlist], Tlist = Append[Tlist, T]]) &, alist], {i,i1, i2}], {3}]; Show[Graphics[Map[Line[Table[z = homography[#, R Exp[I t]]; {Re[z], Im[z]}, {t, 0, 2 Pi, dt}]] &, Tlist], AspectRatio -> Automatic]] The left image uses a knotted surface pattern that was inspired after Bathsheba Grossman’s beautiful Quin Pendant Lamp, with permission from Bathsheba. Knotted surfaces like this can be extended to cover all kinds of arbitrary surfaces. |

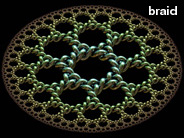
 Hyperbolic tilings can also be visualized using circles. The left picture shows the (7,3) Poincaré hyperbolic tiling rendered using bubbles (an idea which Roger Bagula suggested to me). This is only possible using tilings with 3 polygons meeting at each vertex because bubble intersections must always meet at exactly 120° angles. Here is some Mathematica code to make a Poincaré tiling of tangent circles (you must run the above code before you can run this code):
Hyperbolic tilings can also be visualized using circles. The left picture shows the (7,3) Poincaré hyperbolic tiling rendered using bubbles (an idea which Roger Bagula suggested to me). This is only possible using tilings with 3 polygons meeting at each vertex because bubble intersections must always meet at exactly 120° angles. Here is some Mathematica code to make a Poincaré tiling of tangent circles (you must run the above code before you can run this code):(* runtime: 3 seconds *) abs[z_] := Sqrt[z Conjugate[z]]; ReflectCircle[T_, {z_, r_}] := Module[{z1 = homography[T, z + r], z2 =homography[T, z + I r], z3 = homography[T, z - r], z0, r0}, {z0, r0} /. Solve[{abs[z1 - z0] == abs[z2 - z0] == abs[z3 - z0] == r0}, {r0, z0}][[1]]]; Show[Graphics[Map[({z, r} = ReflectCircle[#, {0, 1}]; Circle[{Re[z], Im[z]}, r]) &, Tlist], AspectRatio -> Automatic]] |
 I am selling mousepads using these designs here. Please email me if you are interested in purchasing this design on other formats (rugs, door mats, placemats, handbags, etc.)
I am selling mousepads using these designs here. Please email me if you are interested in purchasing this design on other formats (rugs, door mats, placemats, handbags, etc.) |
Mathematica code - for animated Poincaré grid, by Matthew Cook C# code for AutoCAD - by Kean Walmsley Circle Limit III and Circle Limit IV - famous hyperbolic tessellations by M.C. Esher “Escher Fish” - Mathematica version by Silvio Levy Kangaroo Tiling - hyperbolic tessellation by Guy Cousineau, et. all |
Conformal Mappings of the Poincaré (7,3) Hyperbolic Tiling - AutoLisp, POV-Ray 3.6.1, 5/10/11

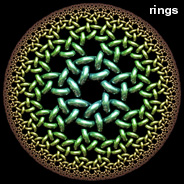
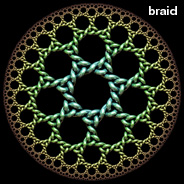
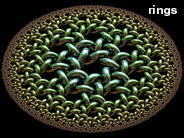
 There are many ways to distort an image, but conformal mapping is the only method that preserves angles. Poincaré disks are especially great for conformal mapping, because they represent a conformal projection from hyperbolic space to Euclidean space. Here are some examples of conformal mappings to multi-curl (or "murl" as described by Zueuk), rings, squares, regular polygons, and hearts. The images with a knotted surface pattern were inspired after Bathsheba Grossman’s beautiful Quin Pendant Lamp. See also my recursive Poincaré fractal.
There are many ways to distort an image, but conformal mapping is the only method that preserves angles. Poincaré disks are especially great for conformal mapping, because they represent a conformal projection from hyperbolic space to Euclidean space. Here are some examples of conformal mappings to multi-curl (or "murl" as described by Zueuk), rings, squares, regular polygons, and hearts. The images with a knotted surface pattern were inspired after Bathsheba Grossman’s beautiful Quin Pendant Lamp. See also my recursive Poincaré fractal.Conformal Mapping Links Ringworld - French article on hyperbolic ring tilings, by Jos Leys, see also his gallery Sporogenesis, Blooming - beautiful multi-curl Poincaré tessellations, by Zueuk Schwarz-Christoffel Mapping - method for mapping arbitray shapes Conformal map for regular polygon in circle - Physics Forums discussion Peirce's Quincuncial Map - maps to a square Kaleidoscopes - includes some hexagon and square mappings of the Poincaré disk, by Vladimir Bulatov, see also his Google+ posts Smarties: Pointy Heart - by Gadl |
Conformal Mappings of the Poincaré (6,4) Hyperbolic Tiling - C#, 5/16/11
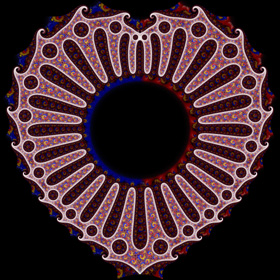
 Here are some more complicated conformal mappings of the Poincaré disk. Click here for a more detailed explanation.
Here are some more complicated conformal mappings of the Poincaré disk. Click here for a more detailed explanation.Conformal Mapping Links Drost Effect - article by Jos Leys |


|
Hyperbolic Dodecahedron - POV-Ray 3.6.1, 2/15/07

 Hyperbolic polyhedrons can be visualized in Euclidean space using sphairahedrons (polyhedrons with spheres for each face). This picture shows a hyperbolic dodecahedron composed of 12 spherical faces. This image was featured on the cover of McGraw-Hill's 2012 & 2013 Geometry textbooks. Click here to download some POV-Ray code for the hyperbolic dodecahedron.
Hyperbolic polyhedrons can be visualized in Euclidean space using sphairahedrons (polyhedrons with spheres for each face). This picture shows a hyperbolic dodecahedron composed of 12 spherical faces. This image was featured on the cover of McGraw-Hill's 2012 & 2013 Geometry textbooks. Click here to download some POV-Ray code for the hyperbolic dodecahedron.<< Graphics`Polyhedra`; Show[Graphics3D[Polyhedron[Dodecahedron][[1]]]] Links Ideal Hyperbolic Polyhedra - POV-Ray renderings by Matthias Weber Dodecahedral Machinery - by Ramiro Perez Spikey - Mathematica’s cover image dodecahedron Megaminx - dodecahedron-shaped Rubik's Cube George Hart - polyhedra artist |
Inside the Mirrored Hyperbolic Dodecahedron - POV-Ray 3.6.1, 2/15/07

 This is what the dodecahedron would look like viewed from the inside with spherical mirrored walls. At certain dihedral angles, this resembles the inside of the Poincaré ball (although not exactly). Notice that when the space becomes elliptic, a black “hole” opens up in the center. This is because the space loops around on itself causing objects beyond the “maximum distance” to appear larger because they are actually closer. Weird huh?
This is what the dodecahedron would look like viewed from the inside with spherical mirrored walls. At certain dihedral angles, this resembles the inside of the Poincaré ball (although not exactly). Notice that when the space becomes elliptic, a black “hole” opens up in the center. This is because the space loops around on itself causing objects beyond the “maximum distance” to appear larger because they are actually closer. Weird huh?Links Hyperbolic Chamber - explantion and visuals Legos, by Jos Leys Platonic Solids Kaleidoscope - by Laszlo Bardos |
Inside the Mirrored Flat (Euclidean) Dodecahedron - POV-Ray 3.6.1, 2/12/07



 Here is a dodecahedron viewed from the inside with flat mirrored walls. I have been working on building one of these for years, until I recently discovered DeepLight, which is an absolutely beautiful design by David Hughes and Neil Merchant.
Here is a dodecahedron viewed from the inside with flat mirrored walls. I have been working on building one of these for years, until I recently discovered DeepLight, which is an absolutely beautiful design by David Hughes and Neil Merchant. |
Breather Pseudosphere - new version: POV-Ray 3.6.1, 6/21/06
old version: Mathematica 4.2, MathGL3d, POV-Ray 3.6.1, 9/30/04

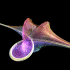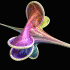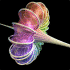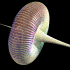 A sphere is an elliptic surface with constant positive curvature. A pseudosphere is a hyperbolic surface with constant negative curvature. This pseudosphere is called a Breather. The animation shows how the surface changes from Kuen's surface into a breather with many ribs when the parameter is changed. Click here to download some POV-Ray code for this image and here for some AutoLisp code. Here is some Mathematica code:
A sphere is an elliptic surface with constant positive curvature. A pseudosphere is a hyperbolic surface with constant negative curvature. This pseudosphere is called a Breather. The animation shows how the surface changes from Kuen's surface into a breather with many ribs when the parameter is changed. Click here to download some POV-Ray code for this image and here for some AutoLisp code. Here is some Mathematica code:(* runtime: 6 seconds *) a = 0.498888; vmax = 47.1232; w = Sqrt[1 - a^2]; Breather[u_, v_] := Module[{d = a((w Cosh[a u])^2 + (a Sin[w v])^2)}, x = -u + 2w^2 Cosh[a u]Sinh[a u]/d; y = 2w Cosh[a u](-w Cos[v]Cos[w v] - Sin[v]Sin[w v])/d; z = 2w Cosh[a u](-w Sin[v]Cos[w v] +Cos[v]Sin[w v])/d; {x, y, z, {EdgeForm[], SurfaceColor[Hue[v/vmax]]}}]; ParametricPlot3D[Breather[u, v], {u, -10, 10}, {v, 0, vmax}, PlotPoints -> {49, 79}, Compiled -> False] Links Virtual Math Museum - beautiful rendition of this surface by Luc Benard, winning entry on cover of Science Magazine’s 2006 Visualization Challenge POV-Ray Code - by Mike Williams, param.inc Cooling Air Towers - also have a hyperbolic shape |
Poincaré Hyperbolic Tessellation - AutoCAD 2000, AutoLisp, C#, Adobe Photoshop 5.0, 5/24/11

 Technically, it is impossible to map a regular Euclidean tiling to the hyperbolic plane but it can still be done with some distortion. This (6,4) tiling of my Dinosaur tessellation was conformally mapped from a hexagon to a hyperbolic hexagon using a Hypergeometric function.
Technically, it is impossible to map a regular Euclidean tiling to the hyperbolic plane but it can still be done with some distortion. This (6,4) tiling of my Dinosaur tessellation was conformally mapped from a hexagon to a hyperbolic hexagon using a Hypergeometric function. |
(3,∞) Poincaré Hyperbolic Tiling - Mathematica 4.2, 3/17/05
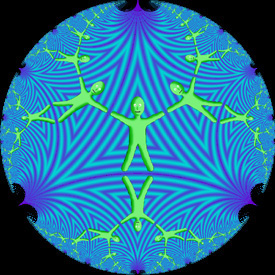

 The area inside this circle represents a hyperbolic plane filled with “ideal triangles”. Notice that all the angles inside these triangles go to zero at the edge of the circle. The right animation shows how a single homography can transform the upper half plane into the Poincaré disk.
The area inside this circle represents a hyperbolic plane filled with “ideal triangles”. Notice that all the angles inside these triangles go to zero at the edge of the circle. The right animation shows how a single homography can transform the upper half plane into the Poincaré disk.Links Reducing Lizards - upper half plane tessellation by M.C. Escher |
Hyperbolic Texture Mapping - left image: C#, POV-Ray 3.6.1, 6/21/11; right image: Mathematica 4.2, C++, 6/22/05


 The Poincaré hyperbolic disk can be conformally mapped to the surface of a sphere. In this mapping, it almost looks like circles are preserved, but not quite. This makes me wonder whether it is possible to conformally map Poincaré disks onto other 3D surfaces. In the left image, the texture was precomputed using forward transformations (this is called the “push forward” method), and then it was mapped to the sphere. In the right image, the the texture was simultaneously calculated using inverse transformations (this is called the “pull back” method) while the sphere was being ray traced. Click here to download a Mathematica notebook for this image. Also, here is some C++ source code for this image.
The Poincaré hyperbolic disk can be conformally mapped to the surface of a sphere. In this mapping, it almost looks like circles are preserved, but not quite. This makes me wonder whether it is possible to conformally map Poincaré disks onto other 3D surfaces. In the left image, the texture was precomputed using forward transformations (this is called the “push forward” method), and then it was mapped to the sphere. In the right image, the the texture was simultaneously calculated using inverse transformations (this is called the “pull back” method) while the sphere was being ray traced. Click here to download a Mathematica notebook for this image. Also, here is some C++ source code for this image. |
(3,∞) Poincaré Hyperbolic Tiling - POV-Ray 3.6.1, 6/22/05

 Click here to download some POV-Ray code for this image. Here is some Mathematica code:
Click here to download some POV-Ray code for this image. Here is some Mathematica code:(* runtime: 0.02 second *) R = Sqrt[3]; Tiles = {Map[1.0 I{{#, R^2 - # Conjugate[#]}, {1, -Conjugate[#]}}/R &, {R + I, -R + I, -2I}]}; Tiles = Append[Tiles, Flatten[Table[Map[Tiles[[1, i]].Conjugate[Tiles[[1, #]]].Tiles[[1, i]] &, DeleteCases[{1, 2, 3}, i]], {i, 1, 3}], 1]]; Do[Tiles = Append[Tiles, Flatten[Table[Map[Tiles[[g, i]].Conjugate[#].Tiles[[g, i]] &, {Tiles[[g - 1, Ceiling[i/2]]], Tiles[[g, 2Ceiling[i/2] - Mod[i + 1,2]]]}], {i, 1, 3×2^(g - 1)}], 1]], {g, 2, 5}]; Tiles = Flatten[Tiles, 1]; n = Length[Tiles]; ToDisk[{{a_, b_}, {c_, d_}}] := Disk[{Re[a/c], Im[a/c]}, Abs[I/c]]; Show[Graphics[{Hue[0], Disk[{0, 0}, 1], Table[{Hue[Sqrt[i/n]], ToDisk[Tiles[[i]]]}, {i,1, n}]}, AspectRatio -> 1, PlotRange -> {{-1, 1}, {-1, 1}}]] |
Hyperboloid - POV-Ray 3.6.1, 6/22/05

 Click here to download some POV-Ray code for this image. You can also make hyperboloids quickly in POV-Ray using the quadric command:
Click here to download some POV-Ray code for this image. You can also make hyperboloids quickly in POV-Ray using the quadric command:camera{location <0,10,0> look_at <0,0,0>} light_source{<0,10,0>,1} quadric{<1,1,-1>,<0,0,0>,<0,0,0>,1 pigment{rgb 1}} Link: Gallery of Algebraic Surfaces - by Xiao Gang |
Other Hyperbolic Links
Curly Kale - interesting animation by Daniel Piker
HypEngine - 3D real-time hyperbolic maze by Bernie Freidin
MagicTile - program demonstrating hyperbolic variation of the Rubik's Cube, by Roice Nelson
Ruffled or Lettuce Sea Slug - hyperbolic surface in nature